Spooky Action at a Distance:
The EPR Experiment with Photons

Quantum theory is a very successful mathematical description of the structure of the atomic and molecular world. But unlike other scientific theories of wide applicability, its interpretation and meaning have been vigorously debated since its inception over seventy years ago. To clarify the unusual stature of quantum theory it might be helpful first to make a list of some of the characteristics we associate with a successful scientific theory.

• Experimental confirmation; predictive success

• Explanatory power; intelligibility

• Internal coherence; aesthetic appeal

• Breadth of applicability; philosophic implications

Scientists agree that quantum theory has received ample experimental confirmation, and that it is a coherent and mathematically appealing theory. In fact quantum mechanics has provided the computational methods and conceptual infra-structure that have catalyzed the impressive progress the physical sciences have experienced in the 20^th century. However, in spite of its experimental validation, many would argue that quantum mechanics does not explain in the traditional sense, that it is not really intelligible, and that it merely offers a mathematical algorithm for making experimental predictions. And, if it has broad philosophic implications they are strange and unsettling to most people.

Basic Postulates of Quantum Mechanics

Before proceeding to the main issue, which is the analysis of an important experiment, it might be helpful to review some of the basic postulates of quantum theory.

1. The wave function, Y, provides a complete description of the physical properties of the system it represents.

2. Systems with the same wave function are identical and indistinguishable.

3. For every observable quantity there is an associated operator.

4. If the wave function is an eigenfunction of an operator the observable quantity represented by the operator has a definite value. Every time a measurement for the observable quantity is made the same value is obtained.

   

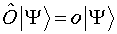
5. If the wave function is not an eigenfunction of a particular operator the system is in a state which does not possess a definite value for the observable quantity associated with that operator. In this case quantum mechanics does not predict with certainty the results of a measurement, but only allows one to calculate (a) the "average value" when many determinations are made, or (b) predict the probability that a particular result will occur. For example, the two equations that follow show how to calculate the average position for a particle in state |Y> and the probability that the particle will be found in the spatial interval from x to x + dx.

   

   

   Richard Feynman captured the significance of this postulate in the following quotation. "A philosopher once said, 'It is necessary for the very existence of science that the same conditions always produce the same results.' Well, they don't!"

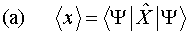
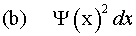
6. After a measurement the wave function of the system is an eigenfunction of the measurement operator.

   As Pascal Jordan has remarked, "Observations not only disturb what has to be measured, they produce it ... We compel the electron to assume a definite position ... We ourselves produce the result of the experiment."

7. Quantum mechanics does not provide a description of what actually happens between two consecutive observations.

   As Heisenberg has succinctly put it, "If we want to describe what happens in an atomic event, we have to realize that the word 'happens' can apply only to the observation, not to the state of affairs between two observations."

The indeterministic nature of quantum mechanics is inherent in the basic principles listed above. Quantum theory says that a system can be in a well-defined state described by its wave function and yet the results of subsequent experiments are not necessarily uniquely determined. For example, if the wave function of a system prior to a measurement is not an eigenfunction of the measurement operator, then a certain prediction of the measurement outcome cannot be made.

This is fundamentally different from the classical view in which an experimental result is always uniquely determined by the state of the system and the forces acting on it. According to classical physics, prior to measurement, every property of a system possesses a definite but unknown value, and experiment or observation merely reveals the value of that previously unknown property. By comparison, quantum mechanics denies the existence of certain physical properties independent of measurement. However, it does not deny, as is frequently erroneously claimed, the existence of the physical object itself in the absence of observation.

What is the reaction to such quantum weirdness? Here are some quotations from those who contributed to the foundation of quantum theory.

• Any one who is not shocked by quantum mechanics has not fully understood it. - Bohr

• I think it is safe to say that no one understands quantum mechanics. Do not keep saying to yourself, if you can possibly avoid it, 'But how can it possibly be like that?' because you will go down the drain into a blind alley from which nobody has yet escaped. Nobody know show it can be like that. - Feynman

• We have always had a great deal of difficulty understanding the world view that quantum mechanics represents. At least I do, because I'm an old enough man that I haven't got to the point that this stuff is obvious to me. Okay, I still get nervous with it... You know how it always is, every new idea, it takes a generation or two until it becomes obvious that there's no real problem. I cannot define the real problem, therefore I suspect that there is no real problem, but I'm not sure there's no real problem. - Feynman

• Quantum mechanics is certainly imposing. But an inner voice tells me that it is not yet the real thing. The theory says a lot, but does not really bring us any closer to the secret of the "old one." I, at any rate, am convinced that He is not playing at dice. - Einstein

• It seems hard to look at God's cards. But I cannot for a moment believe that he plays dice and makes use of 'telepathic' means as the current quantum theory alleges He does. - Einstein

• The mathematical predictions of quantum mechanics yield results that are in agreement with experimental findings. That is the reason we use quantum theory. That quantum theory fits experiment is what validates the theory, but why experiment should give such peculiar results is a mystery. This is the shock to which Bohr referred. - Marvin Chester

However strange it may seem, quantum theory has survived all the experimental tests it has been subjected to. Therefore, if quantum theory is strange, it is because the nano-world of electrons, atoms, and molecules is strange. Quantum mechanics is an accurate mathematical account of the behavior of the physical world at the nano scale.

In what follows an important experiment, stimulated by a thought experiment designed originally by Einstein, Podolsky, and Rosen in 1935, is described. Classical and quantum mechanical interpretations of the results and are offered. The classical interpretation fails to account fully for the experimental results, while the quantum mechanical analysis is in complete agreement with the experiment.

Apparatus

A schematic representation of an apparatus is shown in the figure below in which laser radiation is used to raise calcium atoms to an excited state. On returning to the ground state the calcium atoms emit two photons in opposite directions. The polarization of the photons is determined with a combination of polarizing film and a detector as illustrated in the figure. The polarizing films are oriented randomly in three directions as shown. The relative orientation of the polarizers is 60^o.

                                     

                  +-----------+                         +-----------+
                  |     2     |                         |     2     |
                  | 1       3 | /                     \ | 1   *   3 | 
              Y<--| *         |/      A          B     \|     |     |-->Y 
          __ /    |  \            <------ Ca* ------>         |     |    \__
         |   \    |   \       |\                       /|     |     |    /  |
         |    N<--|    \      | \                     / |     |     |-->N   |
         |        |     \     |                         |     |     |       |
         |        |      o    |                         |     o     |       |
         |        +-----------+                         +-----------+       |
         |                          + - - - - - - +                         |
         + - - - - - - - - - - - - -| Coincidence |- - - - - - - - - - - - -+
                                    |   Counter   |
                                    + - - - - - - +

                                        Figure 1

The polarizers 1, 2, and 3 are oriented at angles of -60^o, 0^o, and 60^o, and selected randomly. Thus the angle between any two polarizers is 60^o.

Experiment

As the calcium atoms are excited by the laser radiation the polarizing films are oriented in a random way, and the detectors record whether or not a photon has arrived. The coincidence counter shown in the figure records whether or not both photons passed through the polarizing films. Note that there are nine possible orientations of the polarizing films: 11, 22, 33, 12, 21, 23, 32, 13, 31.

Results

Case 1. In runs for which the polarizing films are oriented at the same angle (11, 22, 33) the photons behave the same: they both either pass through the polarizers or they are both stopped by the polarizers. In other words, if the left detector registers a photon, so does the right detector, and vice versa.

Case 2. In runs for which the polarizing films are oriented at different angles (12, 21, 23, 32, 13, 31) the photons behave in the same way only 25% of the time. That is they both pass the films 25% of the time, while the other 75% of the time one passes and the other doesn't.

Overall. Because in 1/3 of the runs the photons behave the same and in 2/3 of the runs they behave the same way only 25% of the time, in a large number of runs it is found that the photons behave the same way 50% of the time.

Classical Interpretation

Belief in the doctrine of realism is considered by most scientists to be a necessary pre-condition for scientific inquiry. Realism, for the present purposes, might be described briefly as the philosophical belief that an experimental result is determined by a physical property of the system under study whose existence is independent of the experiment or the experimenter.

Thus, the results reported in Case 1 indicate that the photons have the same polarization. In all cases in which the film orientations are the same both photons either pass or do not pass through the polarizing films.

This can lead one to assume that an intrinsic property of a photon is its ability to pass the polarizing film at the three angles chosen. If this assumption is correct, and it convincingly and simply accounts for the Case 1 data, then eight states are required to account for the behavior of the photons. Each photon can come in eight varieties: YYY, YYN, YNY, NYY, YNN, NYN, NNY, NNN. Here Y (yes) and N (no) specify whether or not the photon will pass through the polarizing film when it is oriented at angles 1, 2, or 3. This view that photons or other systems under study have intrinsic properties which are independent of their measurement, but determine the result of a measurement, is one of the cornerstones of science.

The belief that photons carry information on their polarization along the three orientations of the films would yield the results shown in the table below. There are eight photon states and nine film orientations. Thus there are 72 types of encounters between the photons and the polarizing films as recorded by the detectors and the coincidence counter. The realist position (the one adopted by Einstein, for example) demands that the photons behave the same way 67% of the time (48/72), as is shown in the table. This is clearly not in agreement with the experimental result that overall the photons behave the same way only 50% of the time.

	11	22	33	12	21	13	31	23	32
YYY	Same	Same	Same	Same	Same	Same	Same	Same	Same
YYN	Same	Same	Same	Same	Same	Different	Different	Different	Different
YNY	Same	Same	Same	Different	Different	Same	Same	Different	Different
NYY	Same	Same	Same	Different	Different	Different	Different	Same	Same
YNN	Same	Same	Same	Different	Different	Different	Different	Same	Same
NYN	Same	Same	Same	Different	Different	Same	Same	Different	Different
NNY	Same	Same	Same	Same	Same	Different	Different	Different	Different
NNN	Same	Same	Same	Same	Same	Same	Same	Same	Same

Note that the realist position is in agreement with Case 1 results, but in serious disagreement with Case 2 results. For Case 2 it predicts that 50% of the time the behavior of the photons is the same, when the experimental result is that the photons behave the same only 25% of the time.

Quantum Interpretation

According to quantum theory a photon polarized at some angle q to the vertical direction can be written as a linear combination of a vertically and horizontally polarized photon.

Figure 2

Quantum mechanical first principles enable one to calculate the probability that a photon with polarization q will pass a filter with vertical polarization as follows.

Thus the probability that a photon polarized at an angle q will pass a film with vertical polarization is cos²q. In general we can state that the probability that a photon will pass a polarizer is given by the square of the cosine of the angle its plane of polarization makes with the direction of the polarization of the film.

Now to a quantum mechanical explanation for the results of the experiment. For Case 1 results, the fact that the photons behave in the same way when the detector settings are the same (11, 22, 33) indicates that the photons have the same polarization and, therefore, the same wave function. They are in the same state. This is basically the same as the classical interpretation.

However, for the Case 2 results where the detector settings are different (12, 21, 23, 32, 13, 31) quantum mechanics gives a different explanation. Let's take a specific example. First of all, as Figure 1 shows, the three polarizing films have relative angles of 60^o. Now suppose for the 12 detector orientation that photon A moving to the left passes through its film indicating that it is polarized in that direction. Photon moving to the right has the same polarization and, therefore, the same wave function. It is approaching a film that is polarized at an angle of 60^o to the one that A just passed. Thus, the probability that B will pass its film is cos²60 or 25% in agreement with the Case 2 experimental results described earlier.

Let's take a look at another example. Photon A is absorbed by a vertical polarizer indicating that it is horizontally polarized. Since the photons are in the same polarization state, B is also horizontally polarized. The probability it will pass a polarizer oriented 60^o relative to vertical is,

Thus, the probability that photons A and B behave differently (one is absorbed by its polarizer, the other passes its polarizer) is 0.75, again in agreement with Case 2 results.

Of course this also means that the quantum interpretation is in agreement with the overall result that the photons behave the same way 50% of the time. The films have the same setting 1/3 of time and different settings 2/3 of the time. When the films are set the same the photons behave the same way 100% of the time (either they both pass or they both don't pass). When the film settings are different the photons behave the same way only 25% of the time [(1/3) 100% + (2/3) 25% = 50%].

References:

• N. D. Mermin, "Spooky Actions at a Distance: Mysteries of the Quantum Theory," The Great Ideas of Today, Encyclopedia Britannica, Chicago, 1988, pp 2-53.
• N. D. Mermin, "Bringing home the atomic world: Quantum mysteries for anybody," American Journal of Physics, 49, 940-943, (1981).
• N. D. Mermin, "Is the moon there when nobody looks," Physics Today , 38(4), 38-47, (1985).
• N. D. Mermin, "Quantum mysteries revisited," American Journal of Physics, 58, 731-734, (1990).
• J. C. Polkinghorne, The Quantum World, Princeton Science Library, Princeton, N.J.,1984.
• A. I. M Rae, Quantum Mechanics, 3rd Ed., Institute of Physics Publishing, Bristol, UK, 1992.

Back to Frank Rioux's homepage.