Frank Rioux
Department of Chemistry
St. John's University/College of St. Benedict
Neils Bohr once observed that from the perspective of classical physics the stability of matter was a pure miracle. The problem, of course, is that two of the basic building blocks of matter are oppositely charged particles - the proton and the electron. Given Coulomb's Law the troubling question is what keeps them from coaleseing?
Quantum mechanics is considered by many to be an abstract and esoteric science that doesn't have much to do with everyday life. Yet it provides an explanation for atomic and molecular stability, and classical physics fails at that task. Thus, to achieve some understanding of one of the basic facts about the macro-world requires quantum mechanical concepts and tools.
The issue of atomic stability will be explored with a quantum mechanical analysis of the two simplest elements in the periodic table - hydrogen and helium. Schrödinger's equation can be solved exactly for the hydrogen atom, but approximate methods are required for the helium atom. However, in the pursuit of an explanation for atomic stability it is instructive to use an approximate method to study the hydrogen atom. The approximate method of choice for many quantum mechanical problems is the variation method.
The Hamiltonian energy operator for the hydrogen atom in atomic units is,
![]()
Using a scaled hydrogenic wave function (a = 1 for the exact solution),
![]()
in a variational calculation yields
![]()
where
![]()
and
![]()
Z is the nuclear charge and the scale factor a is the variational parameter in this calculation. It is easy to see that it is a decay constant which controls how quickly the wave function goes to zero as a function of r, the distance from the nucleus. Therefore, it is also intimately related to the average distance of the electron from the nucleus. This is easily seen by calculating the expectation value for the distance of the electron from the nucleus.
![]()
<R> is inversely proportional to a; a is inversely proportional to <R>. The larger the value of a, the closer the electron is on average to the nucleus. Using this relationship <R> can be made the variational parameter as is shown in the equation below.
![]()
The next step in elucidating the nature of atomic stability is to plot EH vs R.
Imagine a hydrogen atom forming as an electron approaches a proton from a great distance. (Notice that we assume that the more massive proton is stationary.) The electron is drawn toward the proton by the Coulombic attractive interaction between the two opposite charges and the potential energy decreases like -R-1. The attractive potential energy interaction confines the electron to a smaller volume and according to deBroglie's wave hypothesis for matter the kinetic energy increases like V-2/3 or as shown above like R-2. Thus the kinetic energy goes to positive infinity faster than the potential energy goes to negative infinity and a total energy minimum (ground state) is achieved at R = 1, as shown in the figure above. The electron does not collapse into (coalesce with) the proton under the influence of the attractive Coulombic interaction because of the repulsive effect of the confinement energy - that is, kinetic energy. Kinetic energy, therefore, is at the heart of understanding atomic stability. But it is important to understand that this is quantum mechanical kinetic energy, or confinement energy. It is remarkably different than classical kinetic energy.
We now move on to the next most complicated element, helium. Helium has a nucleus of charge +2 and two valence electrons. The Hamiltonian energy operator in atomic units is given by,
![]()
There are five terms in the energy operator, but only one new type, the electron-electron potential energy term. When this interaction is calculated using the variational wave function given above we have,
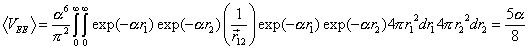
The total energy for helium atom can now be written as shown below because the same relationship applies between <R> and a [a = 3/(2<R>)].
![]()
Graphing EHe vs. <R> reveals again that kinetic energy (confinement energy) is the key to atomic stability. Several things should be noted in the graph shown below. First, that when the total energy minimum is achieved VNE and V (VNE + VEE) are still in a steep decline. This is a strong indication that VEE is really a rather feeble contribution to the total energy, increasing significantly only long after the energy minimum has been attained. Thus electron-electron repulsion cannot be used to explain atomic stability. The graph below clearly shows that on the basis of classical electrostatic interactions, the electron should collapse into the nucleus. This is prevented by the kinetic energy term for the same reasons as were given for the hydrogen atom.
Unfortunately chemists tend to give too much significance to electron-electron repulsion (see VSEPR for example) when it is really the least important term in the Hamiltonian energy operator. And to make matters worse they completely ignore kinetic energy as an important factor in atomic and molecular phenomena. It is becoming increasingly clear in the current literature that many well-established explanations for chemical phenomena based exclusively on electrostatic arguments are in need of critical re-evaluation.
Back to Frank Rioux's homepage.