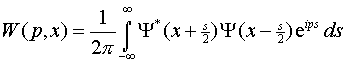
References to the Wigner distribution function1-3 and the phase-space formulation of quantum mechanics are becoming more frequent in the pedagogical and review literature.4-10 References to the Wigner function in the research literature are numerous and two important applications have been reported in the recent literature.11,12 Given its current importance, the purpose of this note is to use Dirac notation to interpret the Wigner distribution.
The Wigner phase-space distribution can be generated from either the coordinate- or momentum- space wavefunction. The coordinate-space wavefunction will be employed here and the Wigner transform using it is given in Eq. (1) for a one-dimensional example expressed in atomic units.
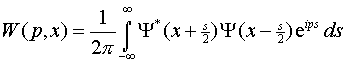
In Dirac notation the first two terms within the integral are written as follows,
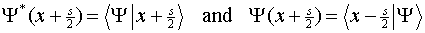
Assigning 1/2p to the third term and employing the momentum eigenfunctions in coordinate space we have,
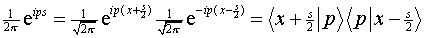
Substituting Eqs. (2) and (3) into Eq. (1) yields after arrangement,
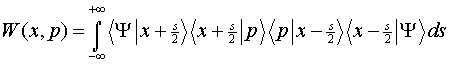
The four Dirac brackets are read from right to left as follows: (1) is the amplitude that a particle in the state Y has position (x - s/2); (2) is the amplitude that a particle with position (x - s/2) has momentum p; (3) is the amplitude that a particle with momentum p has position (x + s/2); (4) is the amplitude that a particle with position (x + s/2) is (still) in the state Y. Thus Eq. (4) is consistent with the description of the Wigner transform as "a convenient mathematical construct for visualizing quantum trajectories in phase space." 9
To see how the Wigner function is integrated using Mathcad click here. To down-load the Mathcad file click here.
To see the Wigner function for the double-slit experiment click here. To down-load the Mathcad file click here.
Literature cited:
Back to Frank Rioux's homepage.